Listen to the article
L’intelligence artificielle (IA) a brillé en maths, avec un niveau médaille d’or aux Olympiades internationales de la discipline, en juillet, mais elle n’a pas que des effets positifs.
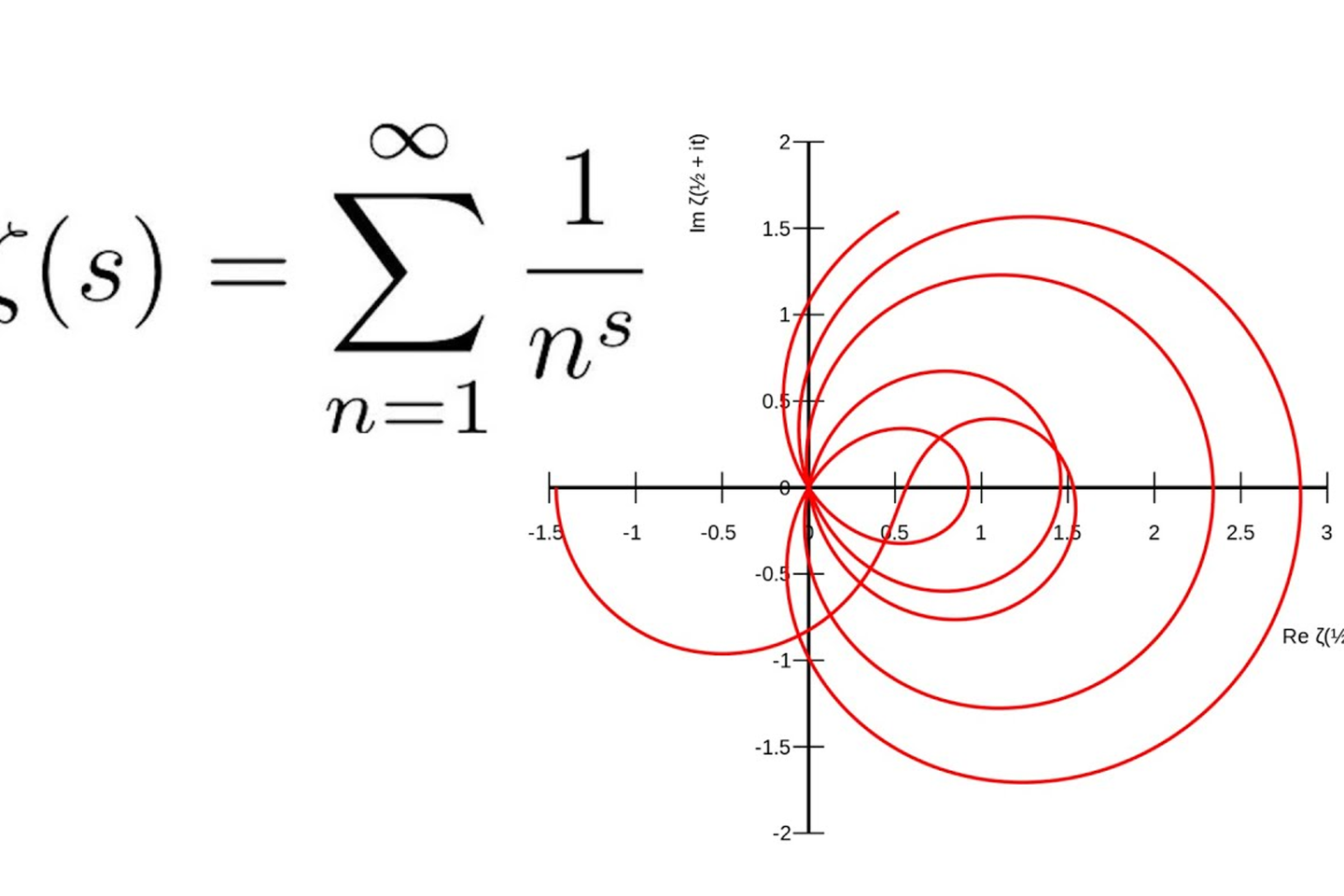
Elle a même commencé à polluer certains forums de spécialistes, revigorant une pratique ancienne : les annonces de démonstration de problèmes célèbres, comme l’hypothèse de Riemann (liée à la répartition des nombres premiers) ou le problème dit « P = NP » (lié à la complexité à résoudre des problèmes), qui sont deux problèmes mis à prix 1 million de dollars (850 000 euros) depuis 2000 par le Clay Mathematics Institute. Mais on pourrait aussi citer le cas de la conjecture de Goldbach ou celle de Syracuse, dite aussi de Collatz (sur les propriétés d’entiers).
Tous les mathématiciens professionnels ont, un jour ou l’autre, reçu de telles « démonstrations » d’amateurs. « Mais là, c’est presque une par semaine ! », a regretté Patrick Massot, professeur à l’université Paris-Saclay, lors d’un colloque consacré aux relations entre IA et maths le 18 novembre à l’Institut Henri-Poincaré. Cette « bouillie » (traduction de l’expression consacrée AI slop) fait « perdre du temps », avait-il ajouté. Il faut dire que le forum qu’il fréquente attire particulièrement les amateurs qui cherchent la renommée. Il est consacré à Lean, un logiciel dit « assistant de preuve », qui est aussi un langage formel, permettant de certifier les enchaînements logiques. Les IA, lors de leur apprentissage, ont donc aussi appris à parler le « Lean » et peuvent faire illusion en fournissant des textes d’apparence correcte.
Il vous reste 56.99% de cet article à lire. La suite est réservée aux abonnés.









16 commentaires
L’IA apporte une nouvelle dynamique aux mathématiques, mais il faut faire attention à ne pas noyer les forums sous des preuves douteuses.
Absolument, cela peut même décourager les vrais contributeurs.
L’IA pourrait être un outil précieux si elle était mieux encadrée dans les débats mathématiques.
Si l’IA peut résoudre des problèmes complexes, pourquoi ne pas utiliser ses compétences pour des défis concrets comme optimiser les chaînes de production dans le secteur minier ?
L’IA pourrait-elle un jour résoudre définitivement l’hypothèse de Riemann ou le problème P = NP ?
C’est ironique que l’IA, capable de prouesses en mathématiques, génère autant de désordre sur les forums spécialisés.
Effectivement, cela montre les deux visages de cette technologie.
Des problèmes comme Goldbach ou Syracuse restent intrigants, même avec l’IA. Peut-être que la solution est à portée de main ?
C’est possible, mais il faudrait une preuve vérifiable.
Les mathématiciens seront-ils capables de filtrer ces démonstrations improvisées à l’avenir ?
La communauté mathématique doit-elle imposer des règles plus strictes pour gérer ces démarches d’amateurs ?
Cela semble nécessaire pour préserver la qualité des échanges.
Ces démonstrations d’amateurs sont-elles vraiment un problème si elles stimulent la discussion ?
Oui, mais à condition qu’elles soient rigoureuses, sinon cela devient une perte de temps.
Ces 1 million de dollars n’ont jamais été aussi tentants, mais faut-il vraiment se fier à des auteurs anonymes ?
La prudence est de mise, surtout lorsque des récompenses financières sont en jeu.